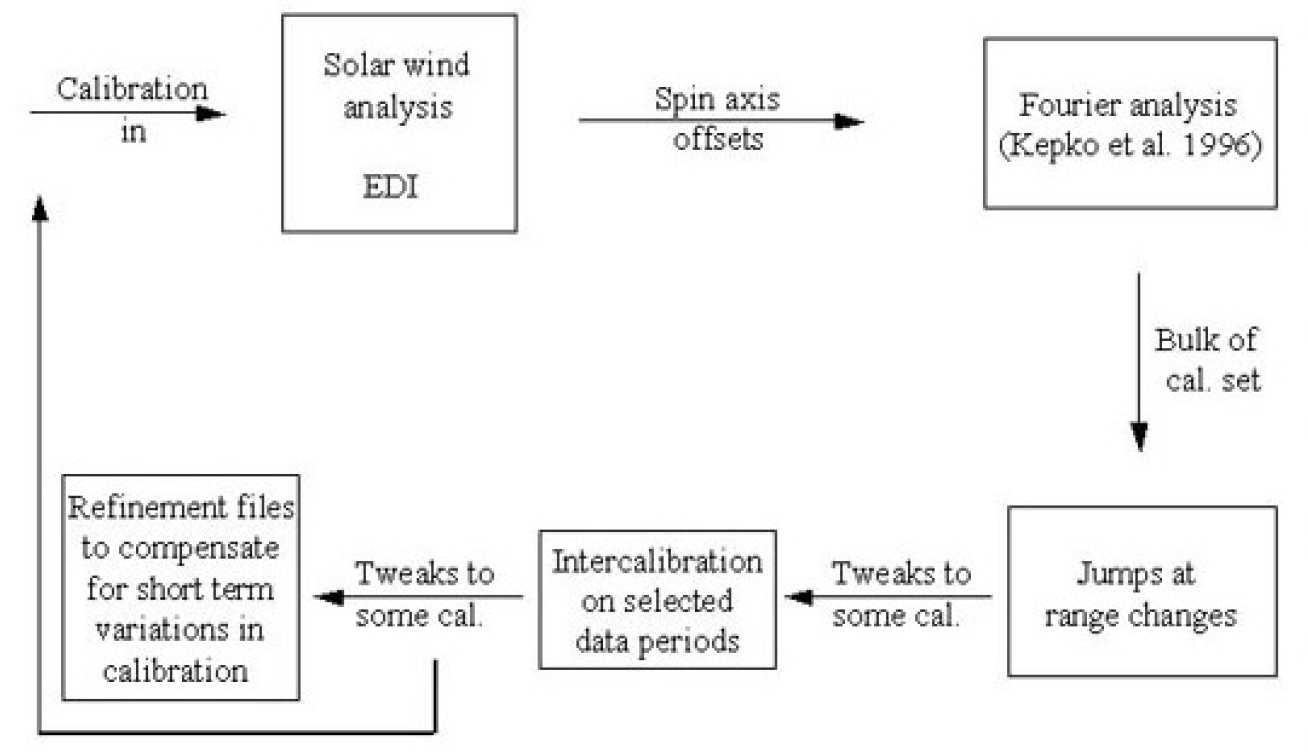
The calibration techniques discussed on this page are designed for use on in-flight magnetometer data from a spinning or set of spinning spacecraft. Specifically the techniques come together to form the ultimate calibration procedure for the data which is to be submitted to the Cluster Active Archive. This calibration procedure is shown in figure 1. Each of the different calibration techniques addresses a calibration parameter or a set of calibration parameters. Using all these techniques together, it is possible to make an estimate or a correction to all of the 12 fundamental calibration parameters set out in the desciption of the calibration problem page.
Fourier Analysis (Kepko et al. 1996)
The Fourier analysis technique is the central calibration method. It can be used to estimate 8 of the 12 calibration parameters although two of the estimations only give relative rather than absolute values. The method is based on the fact that these 8 calibration parameters, when incorrect, produce spin harmonic signatures in the magnetic field data. These spin harmonics can be measured and related to the corrections to the calibration parameters in question. The set of equations which relate the spin harmonics to the corrections to the calibration parameters are solved iteratively and a satisfactory solution is usually obtained within 6-8 iterations.
FGM/EDI comparisons (In collaboration with EDI archive developer, E. Georgescu)
The EDI time of flight measurements can be used to estimate the magnetic field magnitude. This estimation of the magnetic field magnitude can then be used with the FGM magnetic field magnitude to estimate the spin axis offset. Although the errors associated with this method are difficult to deal with, the method has been used to look at the trend of spin axis offsets through time. This method is essential to provide information about the spin axis offsets when the required type of data is not available to use either the solar wind analysis or the intercalibration.
Solar wind analysis (In collaboration with UCLA colleagues, H. K. Schwarzl, K. Khurana, M. Kivelson)
This method uses a specific property of the solar wind in order to provide an estimate for the spin axis offset. The solar wind is known to contain predominantly fluctuations which are rotational in nature. In this case, if the spin axis offset applied is correct, then there is no correlation between the spin axis magnetic field component and the magnetic field magnitude. However if the spin axis offset is incorrect then by removing the resulting correlation, the correction to the spin axis offset can be calculated. In order to obtain good results from this method it is essential to have a good strategy for data selection. Our UCLA colleagues have developed an excellent method which actually utilizes this correlation between the magnetic field magnitude and the magnetic field in the spin axis direction. This method selects solar wind periods which most strongly show the required property and it has been found to produce very accurate results.
Field jumps at range changes (In collaboration with UCLA colleagues, H. K. Schwarzl, K. Khurana, M. Kivelson)
After applying corrections to the spin axis offsets which can be accessed using the solar wind analysis or if no solar wind data is available a different method, and after applying the corrections from the Fourier analysis, jumps in the magnetic field can still be observed in general at instrument range changes. Measuring the field either side of these jumps allows, through a set of equations, fundamental calibration parameters to be modified which up to this stage could not have been estimated. Modifying this set of calibration parameters then reduces the jumps at the rage changes.
Intercalibration (In collaboration with UCLA colleagues, H. K. Schwarzl, K. Khurana, M. Kivelson)
In the paper Khurana et al.(1996) a method is set out which uses the four cluster spacecraft data together in order to modify the remaining calibration parameters which have not been addressed up to this point. The method involves a least squares minimisation which is designed to minimise both divB and curlB in order to calculate corrections to a set of calibration parameters. This method can only be applied in specific regions of the magnetosphere where the current density is expected to be zero, namely the lobes. It is also important that the inter-spacecraft distance is reasonably small. Our UCLA colleagues have established computer code for this method and have supplied us with some intercalibration results which which have been applied to Cluster Active Archive calibration for 2001 magneto tail season data.
Small scale refinement files (In collaboration with UCLA colleagues, H. K. Schwarzl, K. Khurana, M. Kivelson)
The calibration files which are generated using the above methods, in the case of the of Cluster Active Archive calibration, use data which extends over at least one orbit and in the case of some methods significantly longer. This means that the calibration parameters are effectively averaged over a period of time of at least one orbit. It is possible that some calibration parameters can vary over much shorter timescales than an orbit and this can result in small spin harmonic signatures in the calibrated data. The small scale refinement files are designed to take account of these spin harmonic signatures which are left in the data after the other calibration analyses have been performed. The parameters in the refinement files are calculated using shifting time averages of the magnetic field or quantities derived from these averages. This method can modify the standard calibration files on a time scale of 2 minutes and this generally removes the remaining spin harmonic signatures.
References
Kepko E. L., K. K. Khurana, M. G. Kivelson, R. C. Elphic and C. T. Russell, Accurate determination of magnetic field gradients from four point vector measurements: 1. Use of natural constraints on vector data obtained from a single spinning spacecraft, IEEE Trans. Magn., vol. 32, p. 377, 1996.
Khurana K. K., E. L. Kepko, M. G. Kivelson and R. C. Elphic, Accurate determination of magnetic field gradients from four-point vector measurements: 2. Use of natural constraints on vector data obtained from four spinning spacecraft, IEEE Trans. Magn., vol. 32, No. 5, p. 5193, 1996.