Laser Plasma Theory

R.J. Kingham, A.G.R. Thomas, C.P. Ridgers

A new version of the code has also been written, which includes the effects of anisotropic electron pressure. This allows the study of a class of electromagnetic instabilities in the plasma, the simplest case of which is known as the Weibel instability. Better understanding of this instability is very important in laser-plasma applications, as it leads to electron beam filamentation, which is a deleterious effect. The code, and in parallel, an analytic theory has been used to extend our previous models for magnetic field generation to include the effects of anisotropic pressure.

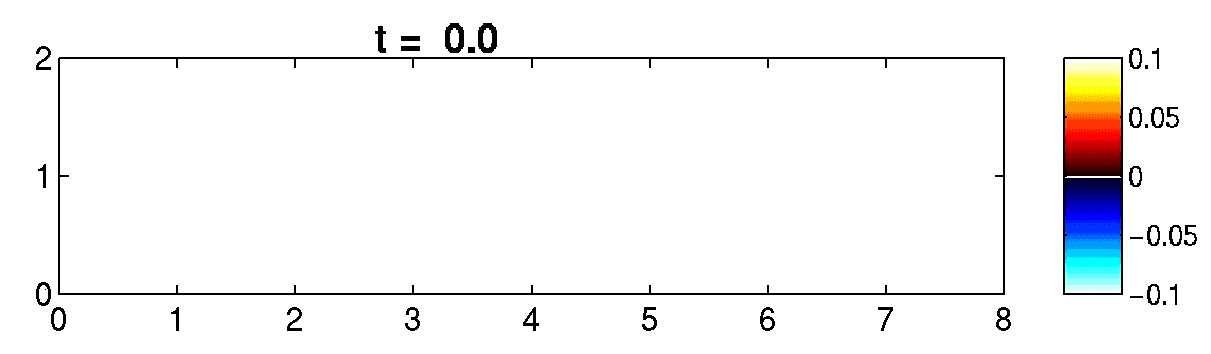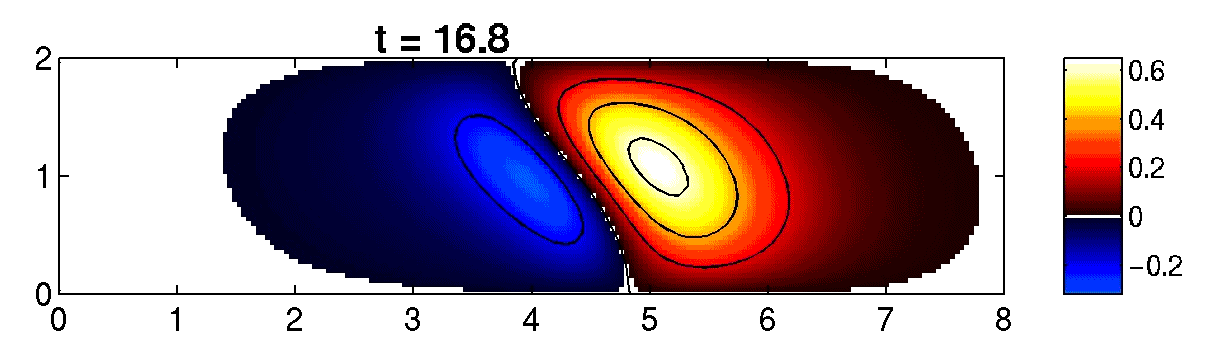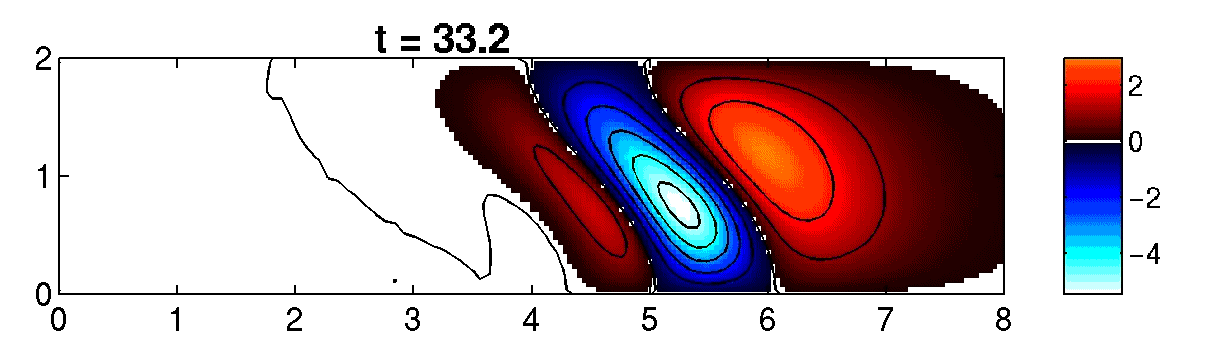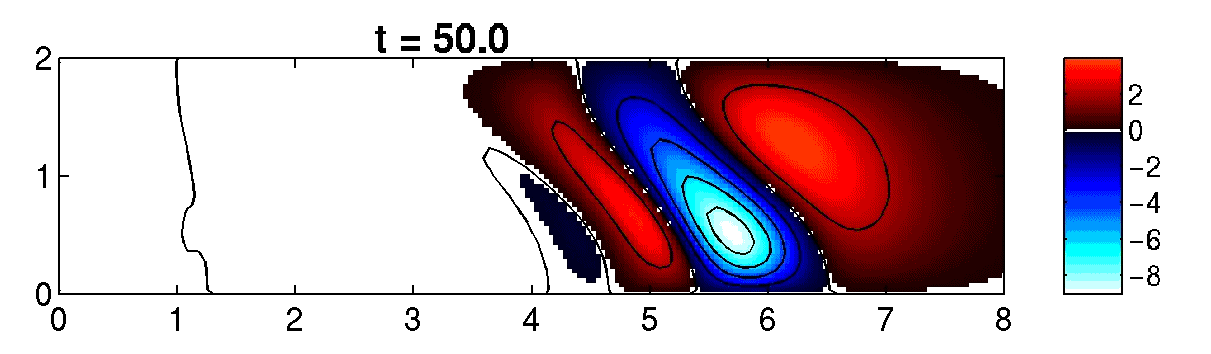
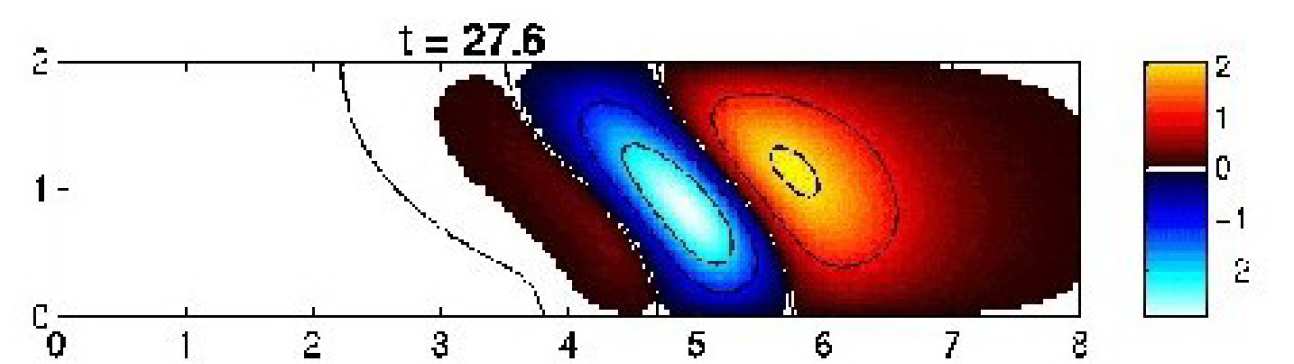
Figure 1 (above right): Magnetic field and electron number density in a laser heated plasma simulated withIMPACT.

Figure 2 (above left): Vlasov-Fokker-Planck numerical modelling of magnetic field generation by non-local effects in a laser heated plasma using IMPACT (see complete animation below).

R. Evans

Most of the equations describing plasma phenomena are inherently non-linear, for example through the jxB force or the strong temperature dependence of the electrical and thermal conductivities. Analytic solutions are only avaialable in some special cases and it is often valuable to solve the underlying equations numerically in order to compare theory and experiment or to establish the sensitivity of measurements to the values of the underlying plasma parameters.

Simulation takes a variety of forms and the simplest models can be run on a laptop computer in a few minutes. More complete plasma models including a kinetic description of the plasma particles and a full solution of Maxwell's equations are hugely demanding and can run for days on large parallel computers with hundreds of compute nodes. The simulations shown here span this range of complexity, the simple fluid model of the plasma imploding around an inserted cone of high density material runs in 20 minutes or so while the 3D particle in cell calculations are at the top end of the computing requirements.

R. Evans

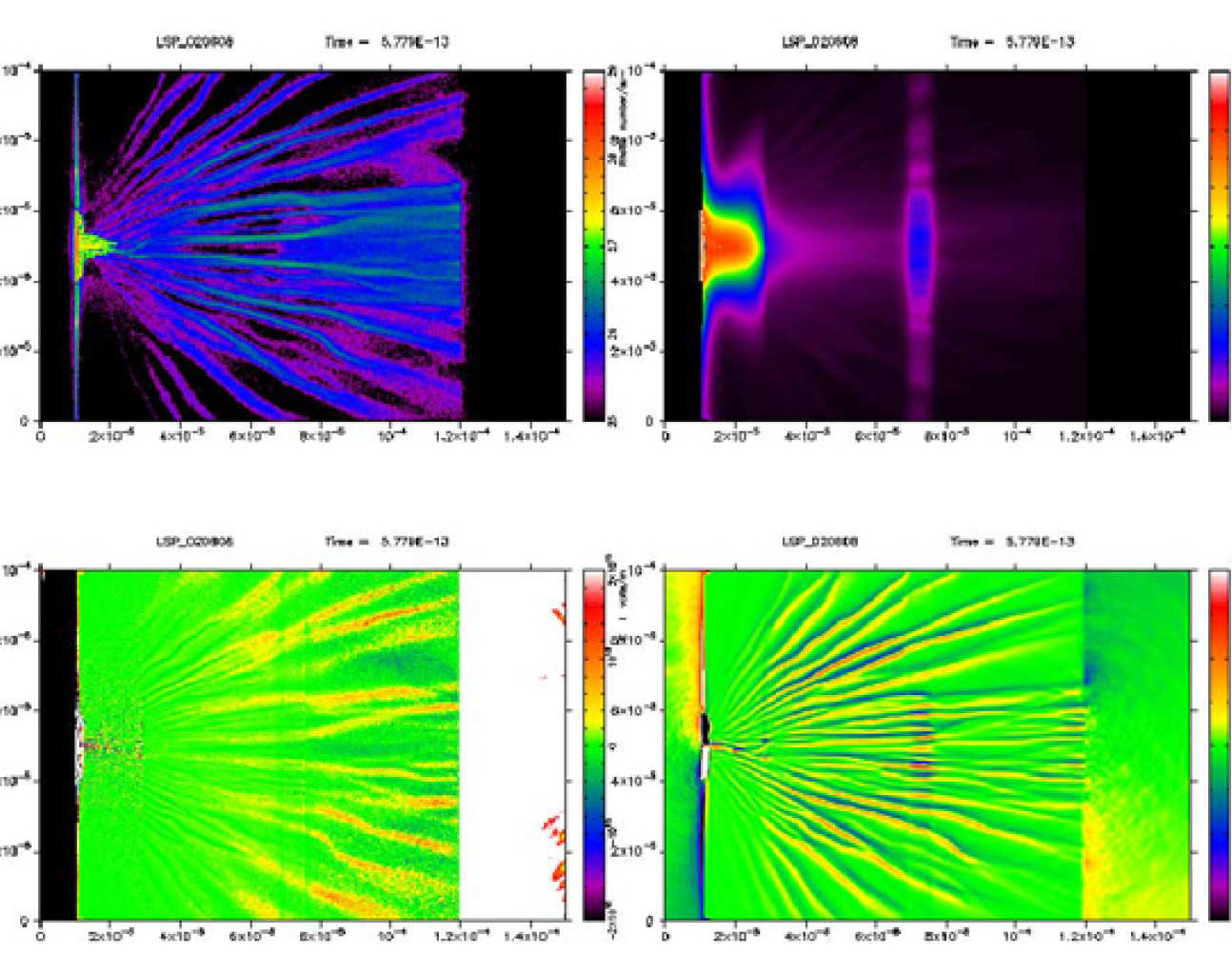
This is a simulation using a hybrid fluid-kinetic treatment of the response of a solid target (the fluid component) to the intense flux of relativistic electrons produced by al ultra short laser pulse. The laser pulse arrives from the left hand side and heats a solid plastic target containing a thin buried layer of Aluminium which serves as temperature indicator in real experiments. The aluminium layer is heated more strongly than the plastic due to its higher resistivity and a magnetic field is generated at the material boundary again due to the gradient in resistivity. The four frames are (clockwise from top left) particle electron density, fluid temperature, magnetic field and electric field.

See full animation below: