In this section

Dr Gerardo Aquino

Biochemistry Building, 301
Tel: +44 (0)20 7594 5054
Email: g.aquino@imperial.ac.uk

Dr. Gerardo Aquino is a research associate in the Biological Physics group working on single receptor and cooperative receptors models of cell sensing, using information theory, bayesian inference and both equilibrium and non-equilibrium statistical mechanics approaches. His main research interests fall within the broad areas of decision making in single cells and modelling complex systems in physics and biology. He also teaches maths to biology master students.

Research projects

Receptors dynamics and physical limits to the accuracy of cell sensing.

Cell sense their environment through 'chemical antennas' , their membrane receptors, proteins which bind and unbind molecules wandering in the external environment. The accuracy with which a cell can sense such chemicals has many limitations due to extra-cellular and intra-cellular noise.

Receptors dynamics and physical limits to the accuracy of cell sensing The fundamental limit of sensing chemicals is due to the external noise from the random arrival of ligand molecules on the cell-surface receptors by diffusion. It is unknown how receptor distribution and dynamics on the cell membrane affect the accuracy of sensing.

Using tools from statistical physics I am studying the effects of receptor clustering, internalization by endocytosis, and diffusion on the accuracy of sensing chemicals. These results will have a large impact in biology by providing quantitative answers to why some receptors exhibit unusual fast diffusion and internalization rates, e.g. in neural synapses, or why ligand-degrading enzymes are located on cell surfaces.

Bayesian inference and filtering in cell sensing of fluctuating environments.

Bayesian inference and filtering in cell sensing of fluctuating environments 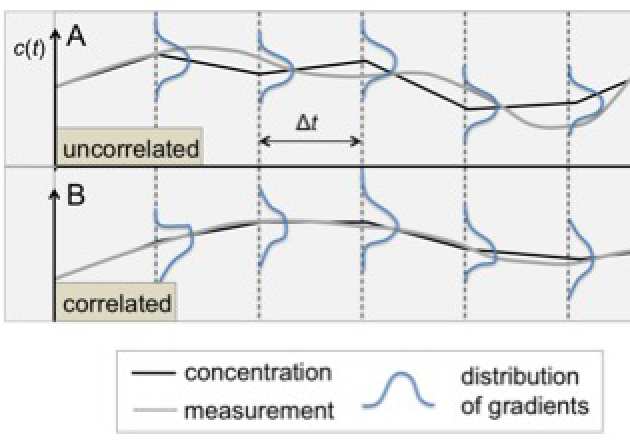Biological cells provide a rich landscape of noise-coping strategies. The physical limit to the accuracy with which cells sense their external environment is ultimately due to the random arrival of external molecules on the cell surface. In this project I model cell sensing in a fluctuating environment as a sequence of measurements of ligand background concentration and slope , each occurring in a given interval of time Δt. A repeated set of measurements is expected to help the cell adjust to changes in the environment based on the track record of past measured values. In Bayesian inference, the knowledge of a prior distribution of the expected values of an observable is known to reduce the lower bound on the variance for the estimate of the same observable. The aim is to determine the improvement to accuracy of cell sensing obtained via sequential estimation and Bayesian inference filtering and to understand how such improvement depends on the statistical properties of the environmental fluctuations. Ultimately, this will shed light on successful cell strategies in environmental adaptation.

Linear Response Theory and ergodicity breakdown

Linear Response Theory and ergodicity breakdown 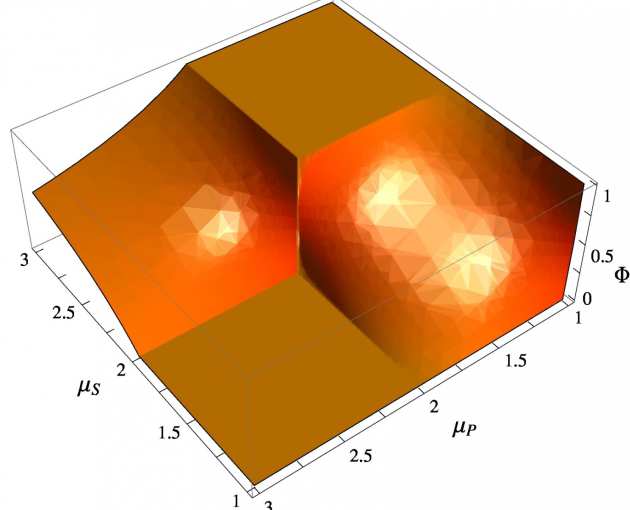How do dissipative systems in non-ergodic regime respond to external perturbation? How does the response depend on the perturbation being deterministic or stochastic and even non-stationary, non-ergodic? All these questions are relevant in systems in critical condition where egodicity-breaking occurs, from interacting neural networks to collective dynamics in swarming and flocking to liquid crystals in the transition to weak turbolent regime.