Basic Dusty Plasmas

Plasma-wall interactions play an important role in plasma physics. In many theoretical studies an infinite unbounded  system is assumed. However, in reality, it is often the case that we need to include the physics of the plasma-wall interaction in order to be able to realistically model a plasma system. Such studies are quite challenging due to the non-linear nature of associated physics.

One such example is the source-collectror sheath system which describes the area between an infinite wall and a Maxwellian source. We assume that plasma is collisionless and ionization free. In such system there are two distinct areas: an electron rich region near the Maxwellian source which is called the source sheath and the other is an ion rich area beside the wall which is called the collector sheath. In the work undertaken by our group in order to model theoretically the source-collector sheath system, we use a truncated Maxwellian distribution for both ions and electrons to describe a collisionless ionization-free plasma and we examine the effect that both stationary and flowing plasmas have on the system. It is the first time in the literature that flows are taken into account in such system. This is very important as it gives further insight about the physics of the system; crucial in cases where flowing plasmas are present, for instance in tokamak divertors like the ones in MAST, JET and ITER.

Our work is both analytical and computational; we benchmark our theoretical model with our simulation results from our Vlasov kinetic code, Yggdrasil, currently being developed at Imperial College London in collaboration with the Rutherford Appleton Laboratory (RAL). Previous numerical studies have used extensively PIC codes for the study of such systems, however the choice of a kinetic code  based on finite difference methods is better as it is less prone to noise thus giving more accurate results obtained from PIC codes.

The most basic model to examine the dust charging process is to assume a spherically symmetric isolated dust grain immersed in a plasma and consider only the effect of electron and ion currents.  However, there are several other charging processes like secondary emission, electron emission, thermionic emission, field emission, radioactivity and impact ionisation. We focus our study on thermionic emission.

When a material is heated, there is an increased probability that an electron from within its structure will have enough energy to leave the volume of the material. This phenomenon is called thermionic emission. Thermionic emission plays a crucial role in many applications. For example, in fusion devices it is an important part of the plasma surface interaction physics of the plasma facing components (PFCs). Furthermore,  thermionic emission is used for the procuction of electrons in many laboratory experiments and in many industrial processes. It plays a central role is high density hot plasmas like the ones created in tokamak reactors.

We extent our previous study to examine the effect that electron emission has on the source-collector sheath system which describes the area between an infinite wall and a Maxwellian source.  In this case, the prefectly absoring wall is replaced with an electron emitting one, giving us the suitable tool to examine the important effect of electron emission. When electron emission is taken into account the situation changes. There are now two different forms of collector sheath, depending on the conditions; one where a potential well is formed and one without a potential well. Our work is both analytical and computational using our Vlasov kinetic code Yggrdrasil. This study is currently being extented from the planar case to the spherical dust grains with the aim to improve our dust transport code DTOKS, developed by the dusty plasma group at Imperial College London.

The charing of large dust grains in the most important process for determining the dynamical behaviour of solid particles of various shapes and sizes. Although in the literature there are several theories for calculating the charge of small dusty grains there is a significant gap in the existing understanding of large dust grains in a flowing plasma. Large dust grains play an important role in dust transport in tokamaks as due to their size can contaminate the plasma.

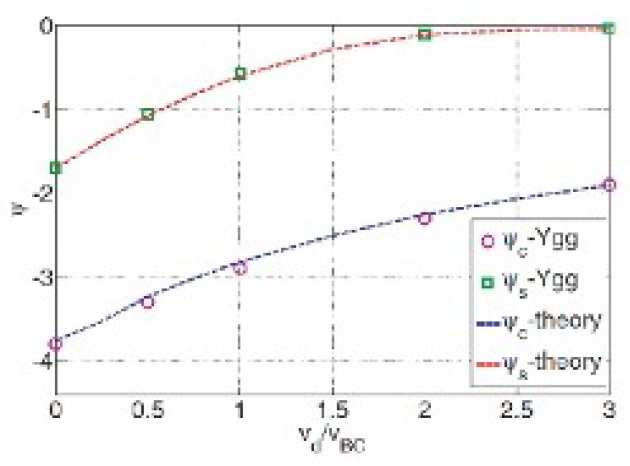
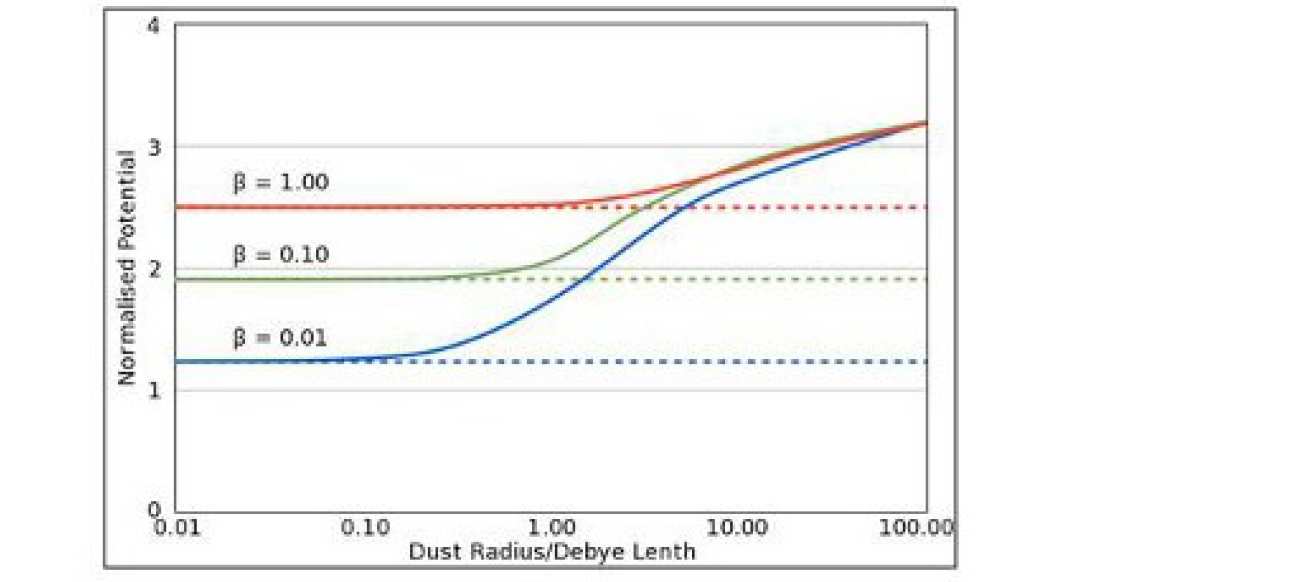
For small dust grains with respect to electron Debye length there is a tried and trusted approach for determining the potential of a grain known as Orbit Limited Theory (OML), for larger grains the OML approach falls down.  In Fig 1 the normalised potential of a dust grain is shown for three values of the ion to electron temperature ratio (beta).  The dashed lines are the prediction of OML, the solid lines are due to a more advanced (and in this case reliable) theory.

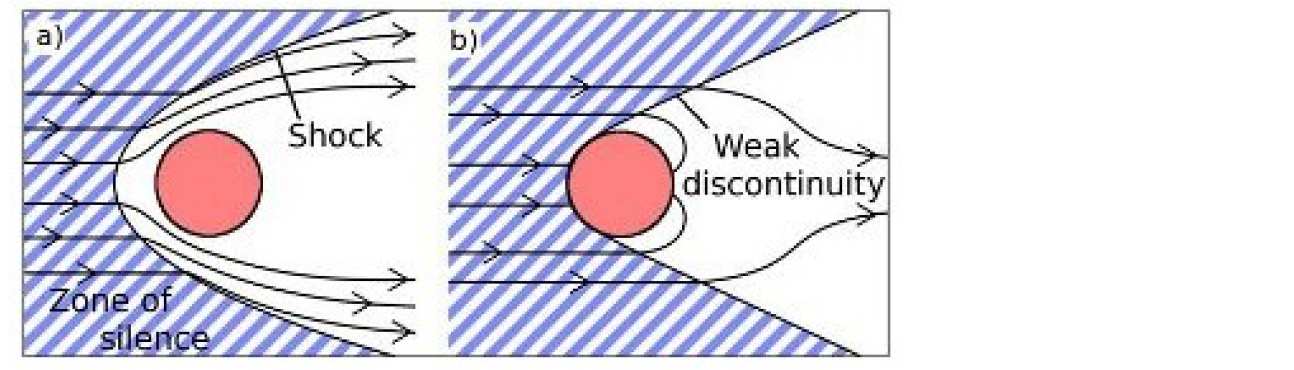
Wake effects are encountered in many areas o f phy si cs with a variety of scale length and complexity.  With dust grains immersed in plasma we see interesting and unexpected effects.  From a compressible hydrodynamics point of view, objects in supersonic flow have been well studied.  These objects are typically non-absorbing and hence the flow must move them around.  A shockwave forms upstream and, depending on the problems geometry, shocks form downstream as the flow converges behind the object. This is represented schematically in Fig 2a.  In the case of dust grains, the impinging flow is simply absorbed, Fig 2b.  The mediating forces are electrostatic and the 'shock-like' formations that form are not shocks at all but weak discontinuities.

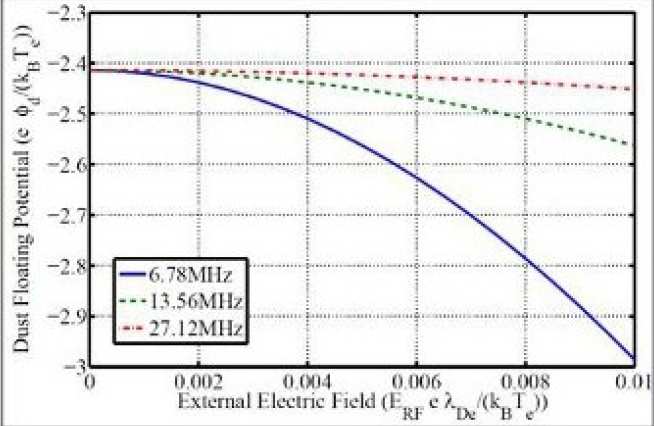
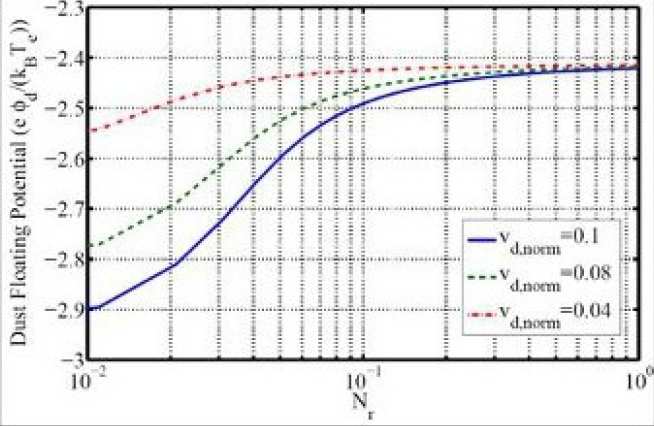
Many dusty plasma experiments and applications involve time varying fields and potentials, for instance experiments in RF discharges where dust particles are either in the sheath or in the bulk plasma o f the discharg e and the study of the Polar Mesosphere Summer Echoes (PMSE) phenomenon in the Earth's mesopause.  Apart from the RF sheath time varying phenomena are also present in the bulk plasma of RF discharges.  The basic formulation of the OML is one of a steady state model.  But how would the charge of a dust grain evolve influenced by the presence of external time varying phenomena?

Our work focuses on time varying phenomena in the bulk plasma of RF discharges.  Two different regimes have been identified.  The first looks into the effect of time varying electric fields to dust grain charging.  It was found that these weak E-fields can alter the shape of the electron distribution function introducing a perturbation that can affect the electron currents to the grain and thus its floating potential.  This approach effectively considers the local conditions prevailing in the dust particle's neighbourhood to deduce its charge.  However, in the wealth of phenomena observed in RF discharges, there are also non-local time varying phenomena (especially for low pressure discharges), where the distribution function in the locality of the dust grain is strongly influenced by conditions far away from the local neighbourhood of the grain.  One such phenomenon, is the observat ion of stochastic heating in low pressure RF discharges.  In this case, the OML approach has been modified to include time varying currents, carried by a small fraction of the electron population stochastically heated in the plasma sheath boundary.

Plasmas often contain liquid droplets, and we term such systems misty plasmas.  Misty plasmas share many properties with conventional dusty plasmas.  For instance, the same charging mechanisms occur.  However, the 'dust grains' are now easily deformable and subject to surface tension, and this gives rise to interesting new effects.

Misty plasmas occur in industrial processes, e.g., plasma-enhanced chemical vapour deposition, and plasma spraying.  It is also known that molten metal droplets occur in tokamaks.  In these plasmas the lifetime of the droplets can be limited by electrostatic effects.

Lord Rayleigh showed that there is a limit to the charge that can be carried by a liquid droplet in vacuo.  Above this the droplet becomes unstable and ejects two very fine jets which carry away a large fraction of the charge but only a small fraction of the mass.  A stable spherical droplet then reforms.

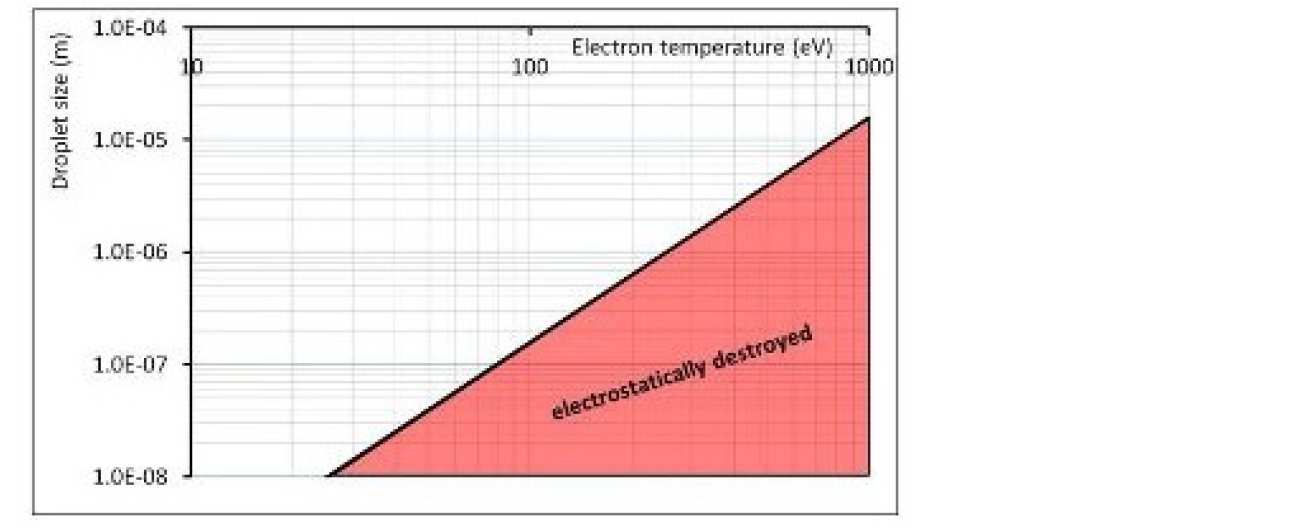
For small droplets (radius less than the plasma Debye length) Rayleigh's result for the critical charge applies in a misty plasma, and his condition can be rewritten in terms of a minimum droplet radius, a_min, which is roughly proportional to the square of the local plasma electron temperature, and inversely proportional to the surface tension of the liquid.  Droplets which fall below a_min cross the Rayleigh threshold and start to disintergrate.  However, in contrast to Rayleigh's droplet in vacuo, the charge on a plasma-immersed droplet is continuously maintained even as the size falls inexorably further below a_min.  Thus a droplet in a misty plasma which crosses the Rayleigh threshold undergoes total electrostatic breakup.  This is faster than evaporation, and therefore limits the survival of small droplets.

Beryllium will be used for much of the inner wall of the ITER tokamak.  Beryllium particles which enter the plasma will rapidly melt.  The fate of one of these molten droplets depends on both its size and the plasma conditions it encounters.  The figure shows the region of parameter space for which Beryllium droplets at their melting point would be destroyed electrostatically.  The Rayleigh mechanism will play a part in determining the lifetime of Beryllium droplets in ITER.